Sir Isaac Newton (1642-1727), English physicist and mathematician, who was the culminating figure of the Scientific Revolution of the 17th century. In optics, his discovery of the composition of white light integrated the phenomena of colours into the science of light and laid the foundation for modern physical optics. In mechanics, his three laws of motion, the basic principles of modern physics, resulted in the formulation of the law of universal gravitation. In mathematics, he was the original discoverer of the infinitesimal calculus. Newton’s Philosophiae Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy, 1687) was one of the most important single works in the history of modern science. (Richard S.Westfall)
Newton’s Laws of motion
Newtons First Law (the law of inertia)
Every object will remain at nest or in a straight-line uniform. motion unless acted upon by an outside force such as friction..
Uniform motion means a constant speed forever. This tendency to remain at a constant speed is called inertia.

Newton’s Second Law of motion (the “force law”)
When a body is accelerated, the acceleration is proportional to the net force acting on the body and inversely proportional to the mass of the body (as one increases, the other one decreases). This explains the relationship between force, mass and acceleration when a net force does act on a body. Forces cause bodies to accelerate (speed up), decelerate (slow down) or change direction. The amount of the acceleration is directly proportional to force acting on the body and inversely proportional to the mass of the body. If you push a body harder it will move faster. and massive bodies need to be pushed harder.

Credit to: Stick man physics
F=ma where F is force (measured in Newtons, N), m is mass (measured in kilograms, kg) and a is acceleration
Acceleration (a) is the change in velocity (Δv) (delta times velocity) over the change in time (Δt), represented by the equation a = Δv/Δt. This allows you to measure how fast velocity changes in meters per second squared (m/s^2).
F=ma
Question 1: If the mass of a huge boulder weighs 454 Kg and the velocity is 5 meters per second what amount of force would it take (in Newtons ) to move the boulder? Answer at end of essay.
I have provided a link to use a force calculator to help you. It is: Calculator Souphttps://www.calculatorsoup.com
a= F/m
Question 2: What acceleration is needed to move a truck weighing one ton if a force of 1200 Newtons is applied.? Hint: one pound = 0.453592 Kg.
Newton’s Third Law
(the”action-reaction law”)
For every action (force) in nature. there is an opposite and equal reaction. The above three laws form the foundation for Newtonian physics.
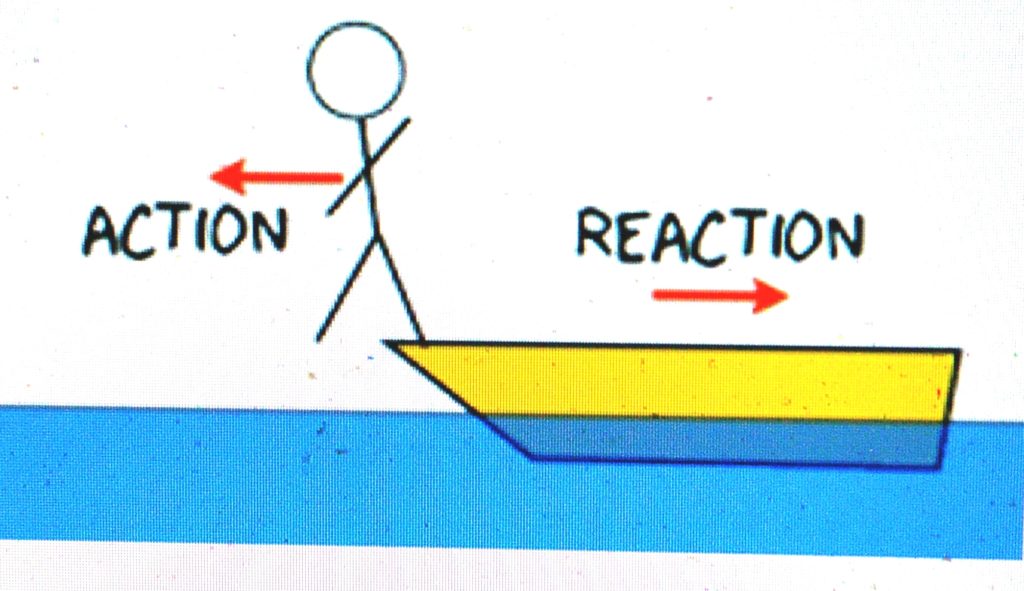
Credit to: WIRED
Newton’s later Fourth Law of Universal Gravitation
Every massive body exerts a force of attraction on every other body that is proportional to the square of the-distance between them.
The larger the masses between two forces, the stronger the attraction and the farther apart they are, the weaker the attraction. Newton used these laws to predict accurately the motion of the planets around the sun and we use them to launch satellites in orbit around the Earth and rockets into space.

Credit to Facebook
Earlier Johannes Kepler (1571-1630) described his Laws of Planetary Motio

First-Law
Planets. move in elliptical orbits (egg shaped) with the sun at one focus.
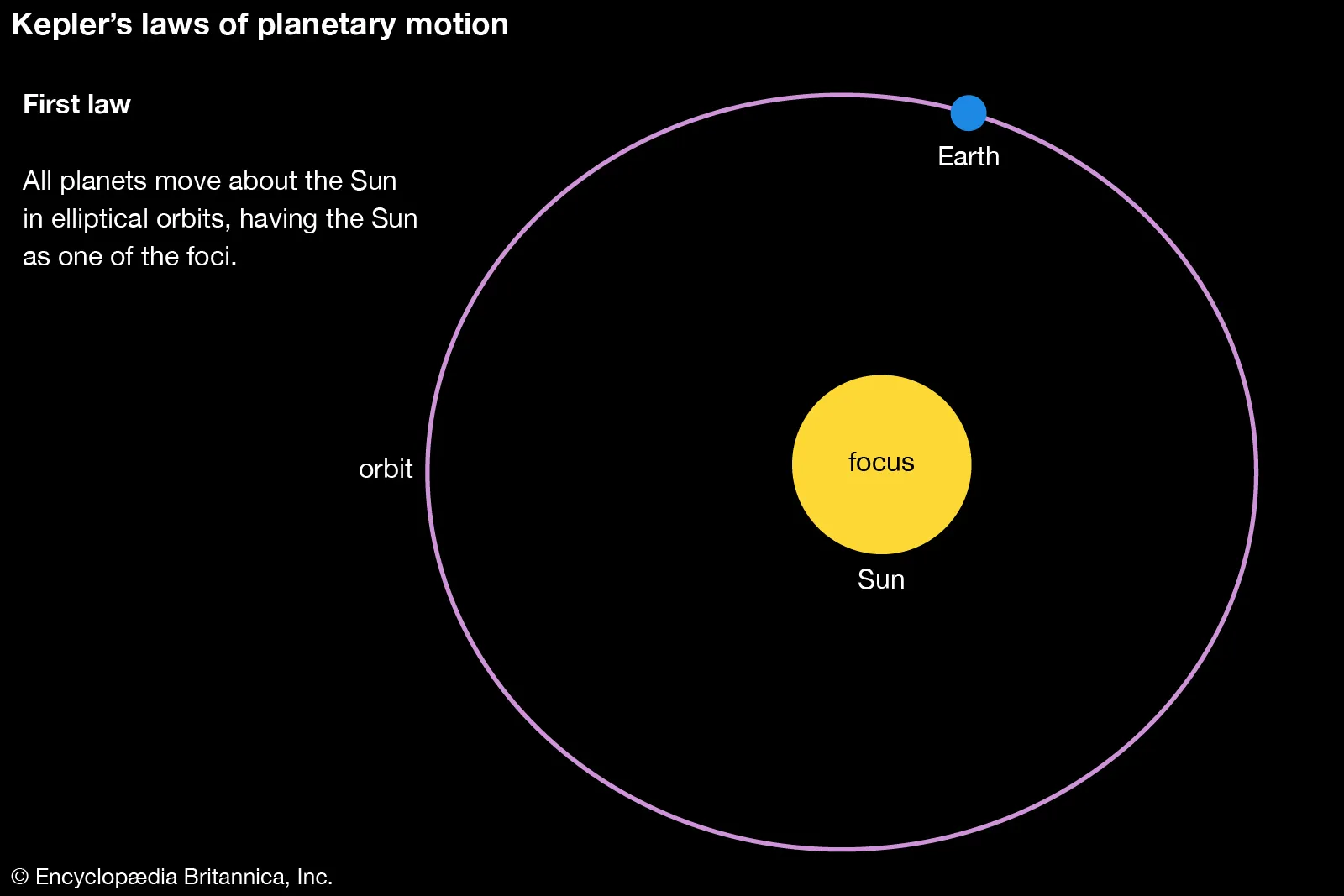
Credit to: Lido
Second Law (the “area law”)
The planets sweep out equal areas in equal times. This means they speed up as they get closer to the sun and slow down as they go farther away. which relates to Newton’s third law. The important thing here is that the area covered in two different separate positions is the same.
.
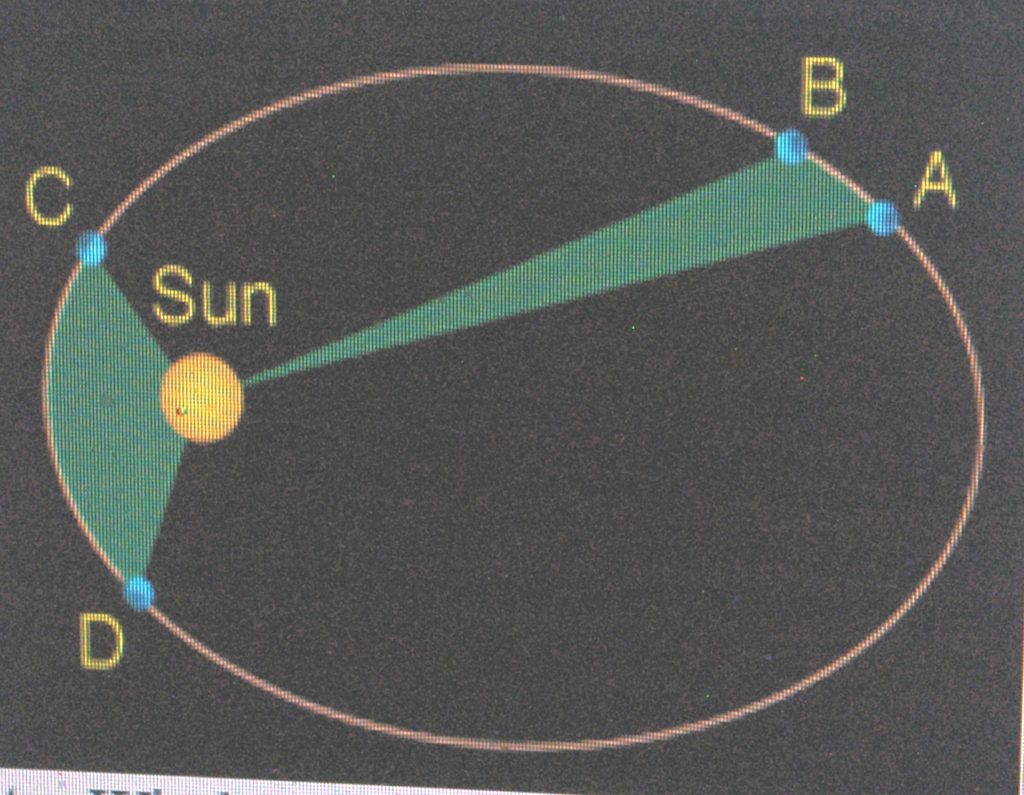
Credit to : NA

Credit to: Windows to the Universe
Third Law (the “harmonic law”)
The square of the orbital period is equal to the cube of the semi- major axis of its orbit. This means that the farther away a planet’s relative position is from the sun in relation to the other planets, the longer will be its year. Thus, earth’s year is 365 days, which is longer than. Venus-which Is longer than Mercury (88 days)
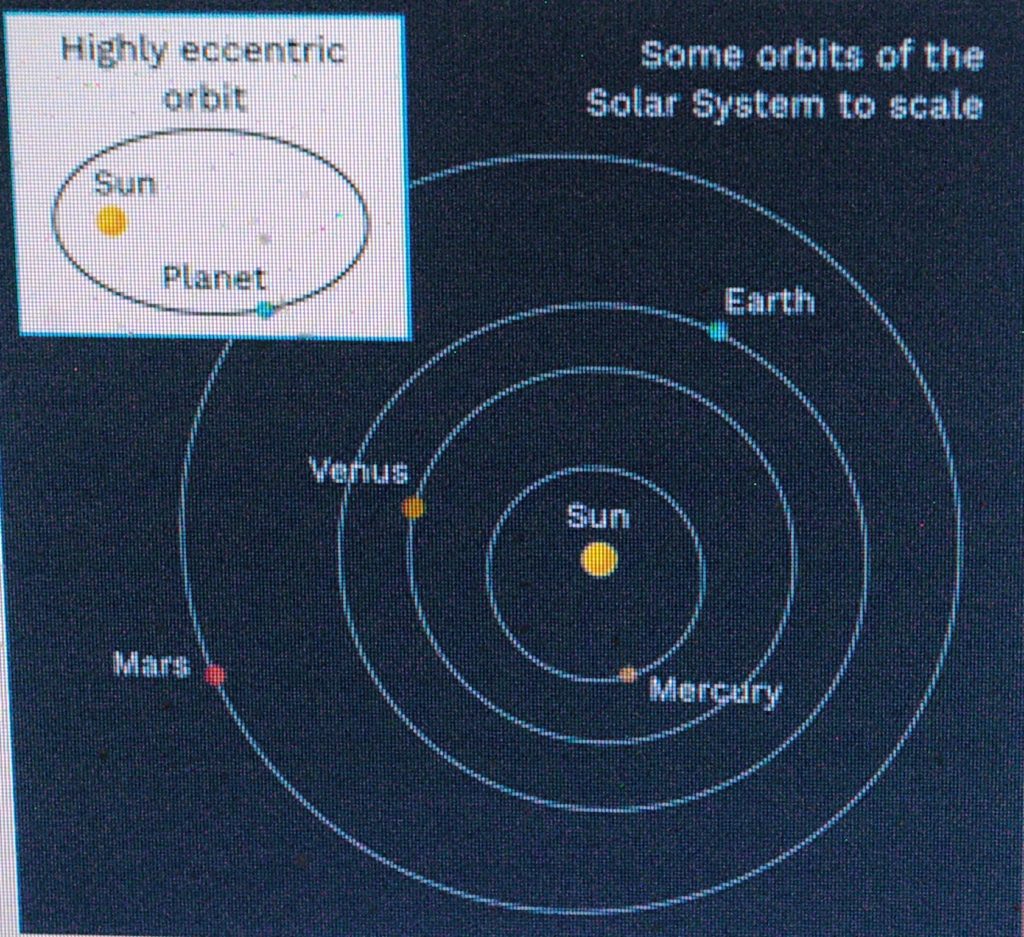
Credit to: Labster
Thus, the square of every planet’s orbital period (years, divided by the cube of its distance is the same (the constant K). Newton, using Kepler’s laws was able to do something that Kepler could not do, and that was to explain his laws. Mathematically. (LaPlante)
The six classical simple machines
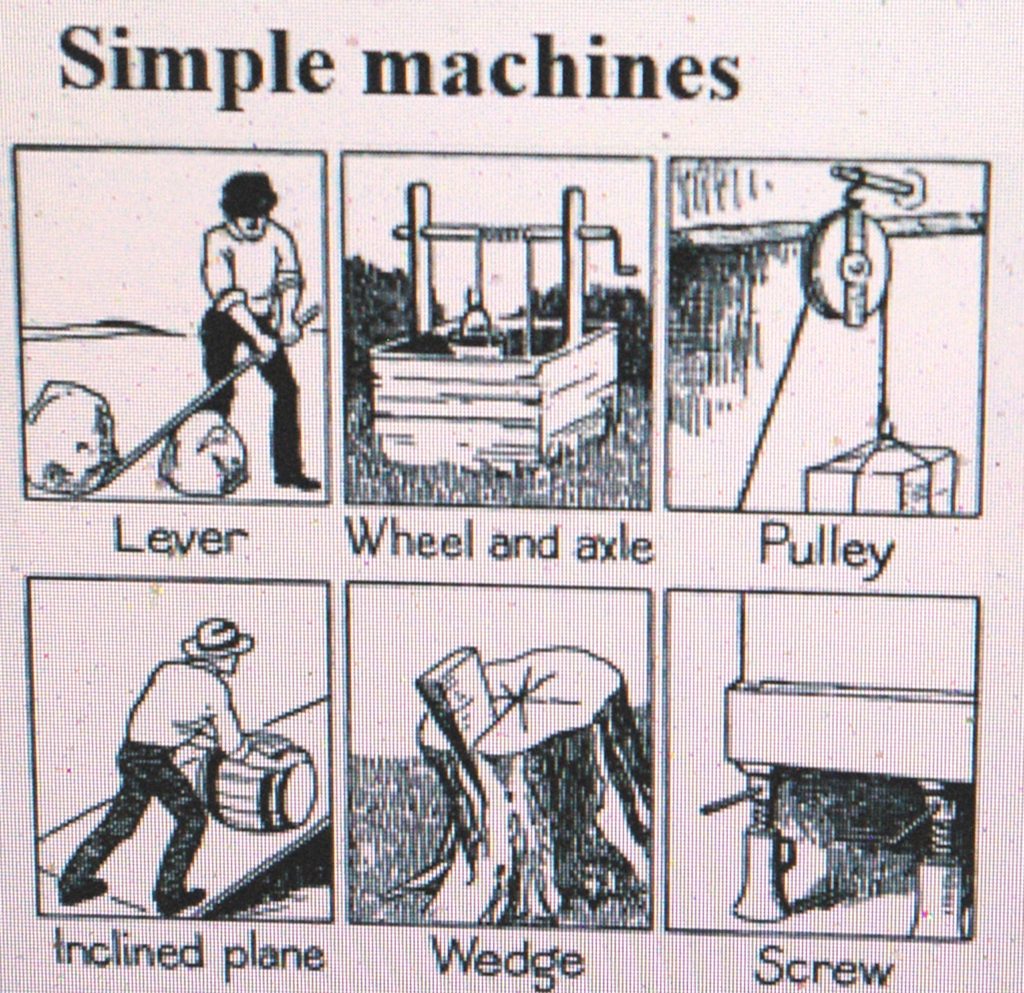
A simple machine is a mechanical device that changes the direction or magnitude of a force. In general, they can be defined as the simplest mechanisms that use mechanical advantage (also called leverage) to multiply force .They include>
A simple machine uses a single applied force to do work (moving an object through a distance). . The machine can increase the amount of the output force, at the cost of a proportional decrease in the distance moved by the load. The ratio of the output to the applied force is called the mechanical advantage.
Simple machines are the “building blocks” of compound machines. For example, wheels, levers, and pulleys are all used in a bicycle The mechanical advantage of a compound machine is just the product of the mechanical advantages of the simple machines of which it is composed.
History
The idea of a simple machine originated with the Greek philosopher Archimedes around the 3rd century BC, who studied the simple machines: lever, pulley, and screw. He discovered the principle of mechanical advantage in the lever. Archimedes’ famous remark with regard to the lever: “Give me a place to stand on, and I will move the Earth” justification was that there was no limit to the amount of force amplification that could be achieved by using mechanical advantage..
Lever
A lever is a simple machine consisting of a beam or rigid rod pivoted at a fixed hinge, or fulcrum. A lever amplifies an input force to provide a greater output force, which is said to provide leverage, which is mechanical advantage gained in the system, equal to the ratio of the output force to the input force. As such, the lever is a mechanical advantage device, trading off force against movement.
A lever is a simple machine consisting of a beam or rigid rod pivoted at a fixed hinge, or fulcrum. A lever amplifies an input force to provide a greater output force, which is said to provide leverage, which is mechanical advantage gained in the system, equal to the ratio of the output force to the input force. As such, the lever is a mechanical advantage device, trading off force against movemen
History
The earliest evidence of the lever mechanism dates back to the ancient Near East circa 5000 BC, when it was first used in a simple balance scale.

A lever is a beam connected to the ground by a hinge, or pivot, called a fulcrum. The ideal lever does not dissipate or store energy, which means there is no friction in the hinge or bending in the beam. In this case, the power into the lever equals the power out, and the ratio of output to input force is given by the ratio of the distances from the fulcrum to the points of application of these forces.
The mechanical advantage of a lever can be determined by considering the balance of moments or torque, T, about the fulcrum. If the distance traveled is greater, then, the output force is lessened. F1 is the input force to the lever and F2 is the output force. The distances a and b are the perpendicular distances between the forces and the fulcrum.
Since the moments of torque must be balanced, the mechanical advantage of the lever is the ratio of output force to input force.
Example
This relationship shows that the mechanical advantage can be computed from ratio of the distances from the fulcrum to where the input and output forces are applied to the lever, assuming no losses due to friction, flexibility or wear. This remains true even though the “horizontal” distance (perpendicular to the pull of gravity) of both a and b change diminish as the lever changes to any position away from the horizontal.
Classes of levers
Three classes of levers

Levers are classified by the relative positions of the fulcrum, effort and resistance (or load). The input force is commonly called “effort” and the output force “load” or “resistance”.
- Class I – Fulcrum is located between the effort and the resistance (toward the middle): The effort is applied on one side of the fulcrum and the resistance (or load) on the other side. Fo
- Examples include seesaw, a crowbar or a pair of scissors, a balance scale, a claw hammer. With the fulcrum in the middle, the lever’s mechanical advantage may be greater than, less than, or equal to 1.
- Class II – Resistance (or load) is located between the effort and the fulcrum (toward the middle): The effort is applied on one side of the resistance and the fulcrum is located on the other side, e.g. a wheelbarrow, a nutcracker, a bottle opener or the brake pedal of a car. Since the load arm is smaller than the effort arm (shorter), the lever’s mechanical advantage is always greater than 1. It is also called a force multiplier lever.
- Class III – Effort is located between the resistance and the fulcrum(toward the middle): : The resistance (or load) is on one side of the effort and the fulcrum is located on the other side, e.g. a pair of tweezers, a hammer, a pair of tongs, a fishing rod, or the mandible of a human skull. Since the effort arm is smaller than the load arm, the lever’s mechanical advantage
Wheel and axle
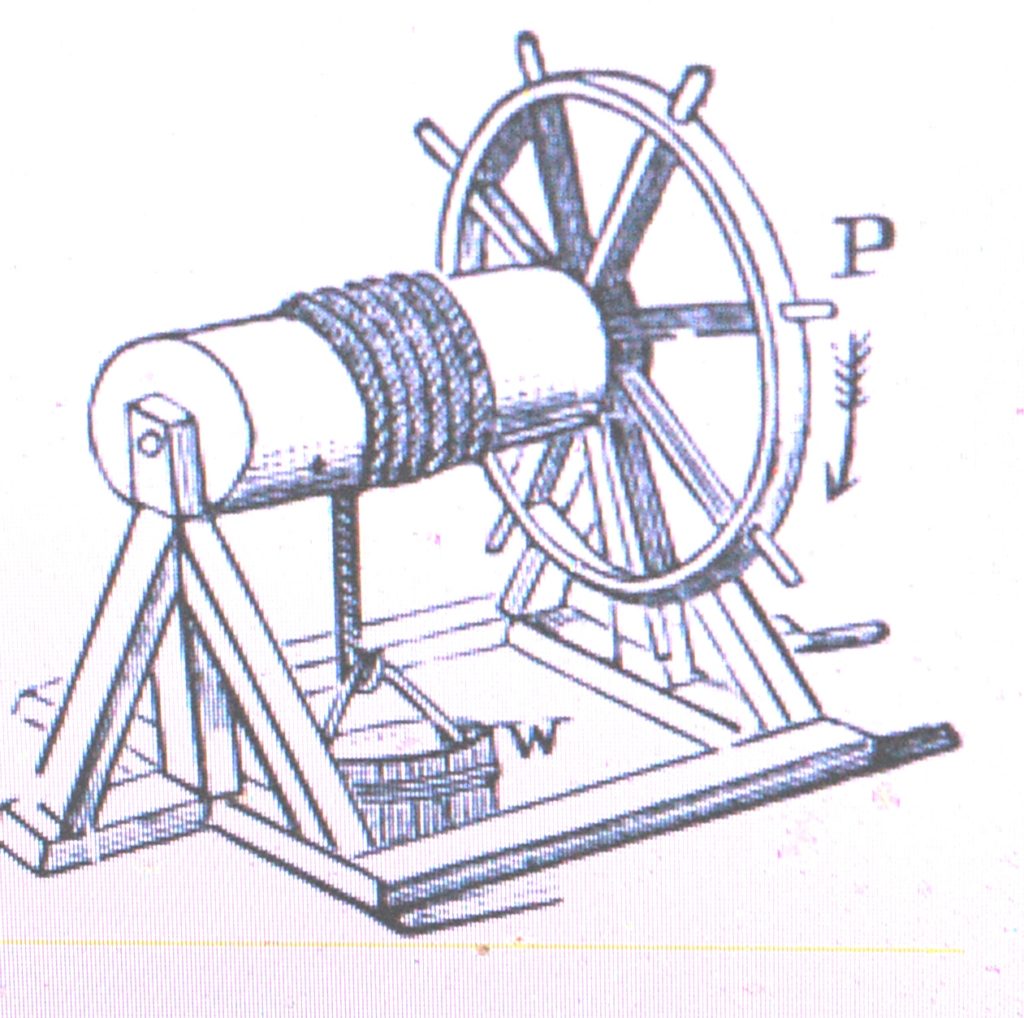
The windlass is a well-known application of the wheel and axle.
The wheel and axle is a simple machine consisting of a wheel attached to a smaller axle so that these two parts rotate together in which a force is transferred from one to the other. The axle and wheel can be viewed as a version of the lever, with a drive force applied tangentially to the perimeter of the wheel, and a load force applied to the axle supported in a bearing, which serves as a fulcrum.
History
The Halaf culture of 6500–5100 BC has been credited with the earliest depiction of a wheeled vehicle, but this is doubtful as there is no evidence of Halafians using either wheeled vehicles or even pottery wheels.
One of the first applications of the wheel to appear was the potter’s wheel, used by prehistoric cultures to make clay pots. The earliest type, known as “tournettes” or “slow wheels”, were known in the Middle East by the 5th millennium BC.
Pulley

Diagram 1: The load F on the moving pulley is balanced by the tension in two parts of the rope supporting the pulley.
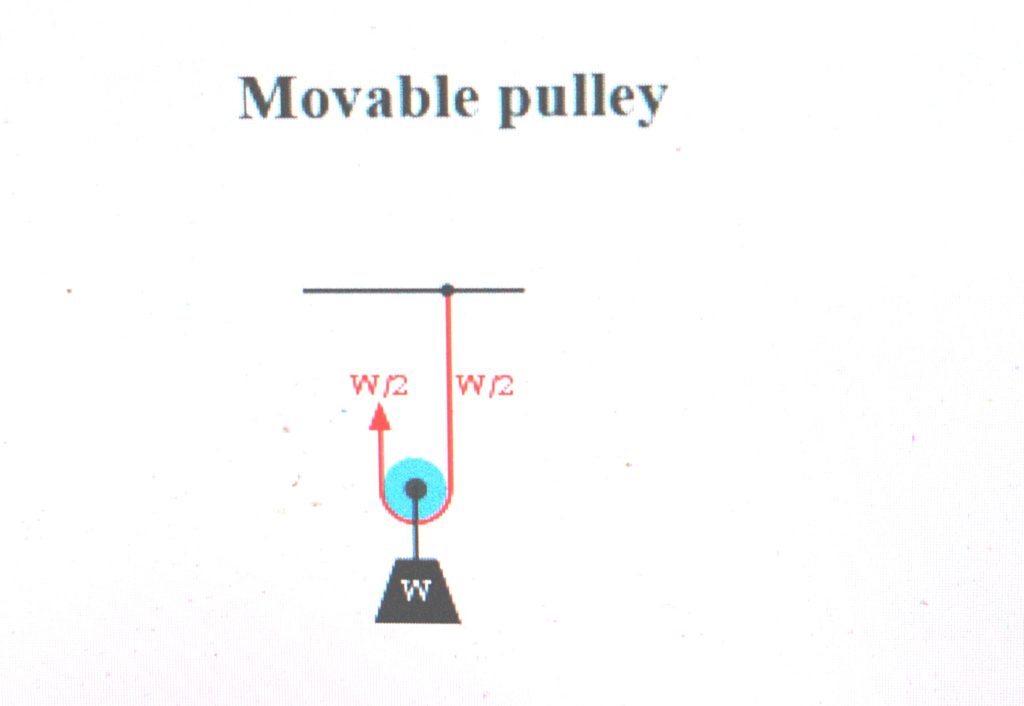
Diagram 2: A movable pulley lifting the load W is supported by two rope parts with tension W/2.
These are different types of pulley systems:
- Fixed: A fixed pulley has an axle mounted in bearings attached to a supporting structure. A fixed pulley changes the direction of the force on a rope or belt that moves along its circumference. Mechanical advantage is gained by combining a fixed pulley with a movable pulley or another fixed pulley of a different diameter.
- Movable: A movable pulley has an axle in a movable block. A single movable pulley is supported by two parts of the same rope and has a mechanical advantage of two.
- Compound: A combination of fixed and movable pulleys forms a block and tackle. A block and tackle can have several pulleys mounted on the fixed and moving axles, further increasing the mechanical advantage.
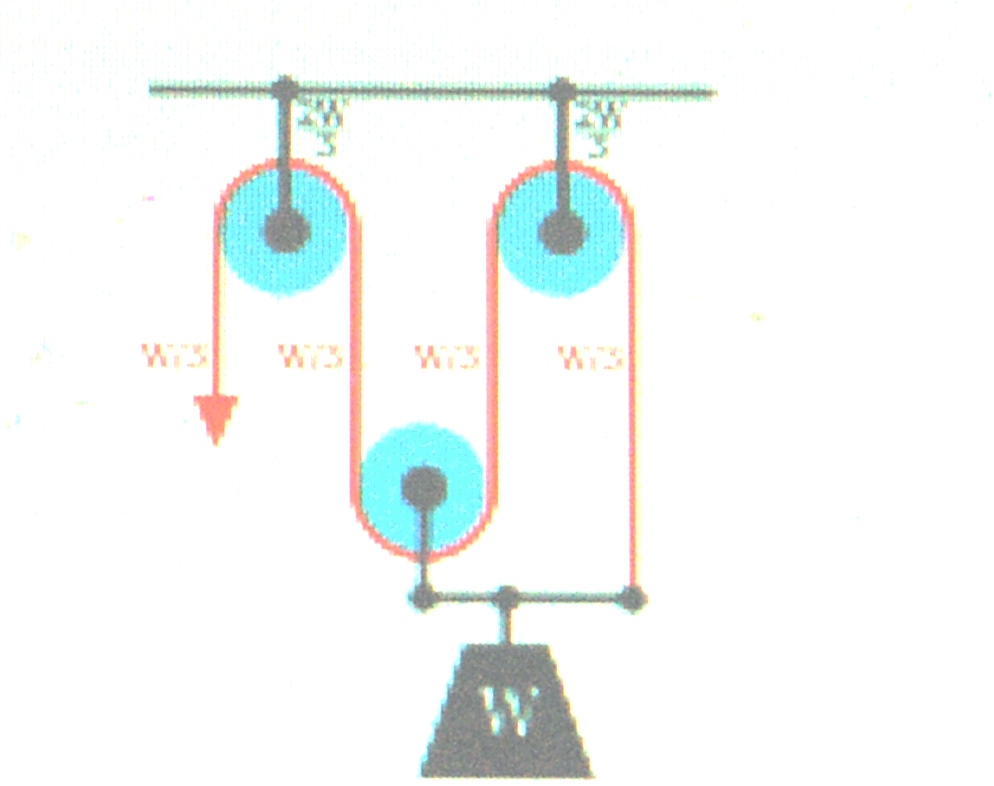
Diagram 3: The gun tackle has the rope attached to the moving pulley. The tension on the rope is W/3 yielding an advantage of three.
The Luff tackle adds a fixed pulley “rove to disadvantage.” The tension in the rope remains W/3 yielding an advantage of three.
The mechanical advantage of the gun tackle can be increased by interchanging the fixed and moving blocks so the rope is attached to the moving block and the rope is pulled in the direction of the lifted load. In this case, the block and tackle is said to be “rove to advantage. Diagram 3 shows that now three rope parts support the load W which means the tension on the rope is W/3. Thus, the mechanical advantage is three.
By adding a pulley to the fixed block of a gun tackle, the direction of the pulling force is reversed though the mechanical advantage remains the same. This is an example of the Luff tackle.

Demonstration inclined plane used in education, Museo Galileo, Florence.
An inclined plane, also known as a ramp, is a flat supporting surface tilted at an angle from the vertical direction, with one end higher than the other, used as an aid for raising or lowering a load.. Inclined planes are used to move heavy loads over vertical obstacles. Examples vary from a ramp used to load goods into a truck, to a person walking up a pedestrian ramp, to an automobile or railroad train climbing a grade.
Moving an object up an inclined plane requires less force than lifting it straight up, at a cost of an increase in the distance moved. The mechanical advantage of an inclined plane, the factor by which the force is reduced, is equal to the ratio of the length of the sloped surface to the height it spans. Owing to conservation of energy, the same amount of mechanical energy (work) is required to lift a given object by a given vertical distance, disregarding losses from friction, but the inclined plane allows the same work to be done with a smaller force exerted over a greater distance.
. This may include cars on rails or pulled up by a cable system; a funicular or cable railway.
Wedge
A wedge is a triangular shaped tool, a portable inclined plane, and one of the six simple machines. It can be used to separate two objects or portions of an object, lift up an object, or hold an object in place. It functions by converting a force applied to its blunt end into forces perpendicular (normal) to its inclined surfaces. The mechanical advantage of a wedge is given by the ratio of the length of its slope to its width. Although a short wedge with a wide angle may do a job faster, it requires more force than a long wedge with a narrow angle.
The force is applied on a flat, broad surface. This energy is transported to the pointy, sharp end of the wedge; hence the force is transported.
The wedge simply transports energy in the form of friction and collects it to the pointy end, consequently breaking the item.

Flint hand axe found in Winchester
Wedges have existed for thousands of years. They were first made of simple stone. Perhaps the first example of a wedge is the hand axe (see also Olorgesailie), which is made by chipping stone, generally flint, to form a bifacial edge, or wedge..
The origin of the wedge is not known. In ancientEgyptian quarries, bronze wedges were used to break away blocks of stone used in construction. Wooden wedges that swelled after being saturated with water were also used. Some indigenous peoples of the Americas used antler wedges for splitting and working wood to make canoes, dwellings and other objects.
Uses of a wedge
The mechanical advantage or MA of a wedge can be calculated by dividing the height of the wedge by the wedge’s width:Wedges are used to lift heavy objects, separating them from the surface upon which they rest.
Screw (simple machine)
. Credit to: Speedway Motors
It consists of a threaded shaft through a threaded hole in a stationary mount. When the crank on the right is turned, the shaft moves horizontally through the hole.
A screw is a mechanism that converts rotational motion to linear motion, and a torque (rotational force) to a linear force.The most common form consists of a cylindrical shaft with helical grooves or ridges called threads around the outside. Wikipedia, the free encyclopedia
The Inverse Square Law
Sound, light, and gravity are examples of forces of physics that spread equally in all directions which describe how the strength of these forces weakens over increasing distance. According to this principle, the effect of the force on an object changes by the inverse square of the distance between the object and the force’s source.
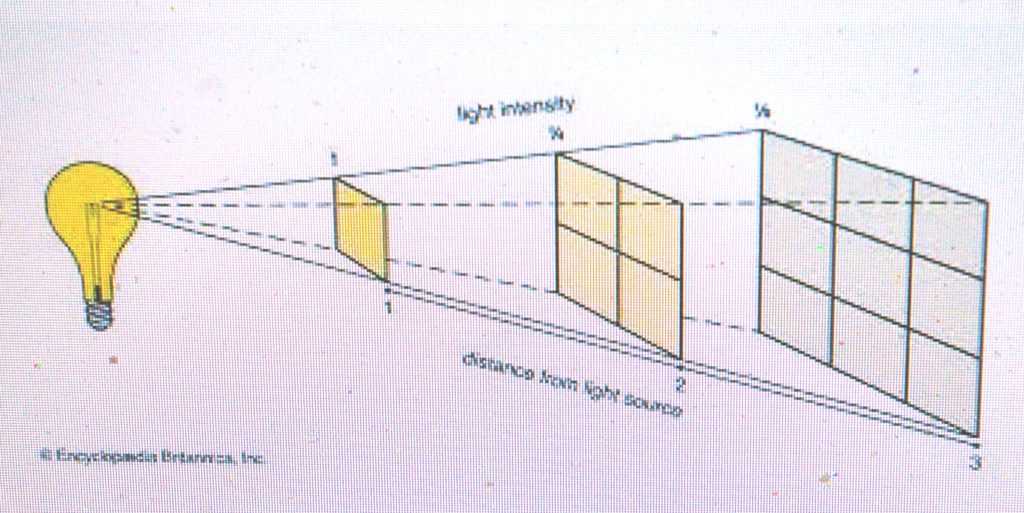
© Encyclopædia Britannica, Inc
In technical terms, an inverse-square law is defined as “any physical law stating that some physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity.” Let’s see how this applies to a field in which one of these physical phenomena, light becomes very important, photography.
In a nutshell, the inverse-square law teaches us how light works over distance and why the distance between your light source and your subject is so important
Let’s say we have a light source which is on full power and our subject is 1 meter away it. If we move our subject double the distance away from the light (2 meters), how much of the light’s power will reach it? The natural reaction is to think “half power” – but unfortunately that’s now how light works, it follows an inverse-square law.
According to the law, the power of the light will be inversely proportional to the square of the distance. So if we take a distance of 2 times and square it, we get 4, the inverse of which would be 1/4 or rather, a quarter of the original power – not half.
Moving our subject 3 meters from the light (3 * 3 = 9, so 1/9) the power of our light source now becomes 1/9th of what it originally was.
In other words, an object placed 30 feet away from a light source will receive only one-ninth (1/32, the inverse of 3 squared) as much illumination as an object placed 10 feet from the light as shown in the following diagrams. By definition, the inverse of any integer (whole number) is turning it upside down, thus making the number the denominator of a fraction with one(1) the numerator, (ie changing 3 to 1/3 and then squaring the resulting fraction, 1/3 X 1/3 = 1/9. Thus, if the brightness of a light bulb ten feet away was 81 lumans, then it would have a brightness of 9 lumans 30 feet away.
Question 3: If the sound of motorcycle was 128 decibels 200 feet away, how loud would it be at quadruple the distance. (answer at the end of the essay.)
.

Credit to: John O’Nolan
The inverse square law shows us how quickly light from our camera flash or flashlight falls off.
References
LaPlant, K. Jul 15, 2019 Examples of Laws of Astronomy and Physics You Tube video The Vocabulary of Science: First Steps to Science Literacy
Westfall, R. https://en.wikipedia.org/Isaac_Newton_(agriculturalist)#:~ :text=Isaac%20Newton%20(agriculturalist,2%20languagesWikipedia Encyclopedia and fast checked by the editors of Encyclopedia Britannica
Question 1 Answer: F = 2,270 N
Question 2 Answer: 1.32 m/s2
Question 3 Answer 8 decibels

